121 Best Time to Buy and Sell Stock

Posted on | In

Intuition

The broute-force solution is listing all the possible combinations and finding the maximum one:

Time complexity for this algorithm is $O(n^2)$. We have linear solution actually, which is not that intuitive. Before talking about the linear solution, let’s see the Largest Sum Contiguous Subarray problem.

Largest Sum Contiguous Subarray

Write an efficient program to find the sum of contiguous subarray within a one-dimensional array of numbers which has the largest sum.

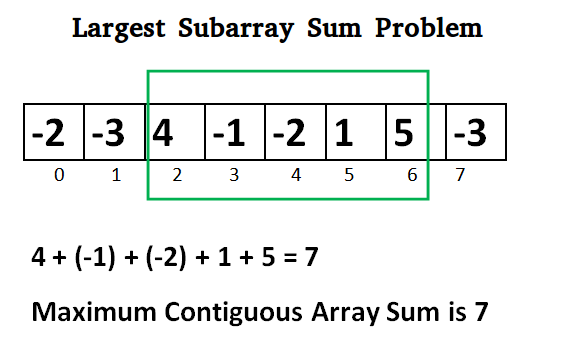
image

The intuitive method for this question is dynamic programming too, but we have more efficient algorithm: Kadane’s Algorithm.

Kadane’s Algorithm keep track of positive sum contiguous subarray, and keep recording a maximum sum among them. For the above array, we have:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
0:
max_segment: -2
max_so_far: -2

1:
max_segment: -3
max_so_far: -2

2:
max_segment: 4
max_so_far: 4

3:
max_segment: 3
max_so_far: 4

4:
max_segment: 1
max_so_far: 4

5:
max_segment: 2
max_so_far: 4

6:
max_segment: 7
max_so_far: 7

7:
max_segment: 4
max_so_far: 7

If the addition of previous segment and current element is positive, we compare the sum with the max_so_far and update previous segment to the addition.

Algorithm

Our goal is to find $max(a[j]-a[i])$, let’s rewrite this formula to

The original question becomes a Largest Sum Contiguous Subarray question! We can get the largest sum within a linear time.

Code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
    public int maxProfit(int[] prices) {
        int max_so_far = 0;
        int max_temp = 0;
        for(int i = 1; i < prices.length; i++){
            int price = prices[i] - prices[i-1];
            if(max_temp + price < 0){
                max_temp = 0;
            }
            else{
                max_temp += price;
                max_so_far = Math.max(max_so_far, max_temp);
            }
        }
        return max_so_far;
    }
}

Complexity

Time Complexity: $O(n)$
Space Complexity: $O(1)$